今天分享的题目来源于 LeetCode 上第 169 号问题：求众数（求数组中超过一半的数字）。题目难度为 Easy，目前通过率为 45.8% 。

最后一种解法 Cool ！！！

题目描述

给定一个大小为 n 的数组，找到其中的众数。众数是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在众数。

示例 1:

输入: [3,2,3]
输出: 3

示例 2:

输入: [2,2,1,1,1,2,2]
输出: 2

题目解析

题目意思很好理解：给你一个数组，里面有一个数字出现的次数超过了一半，你要找到这个数字并返回。

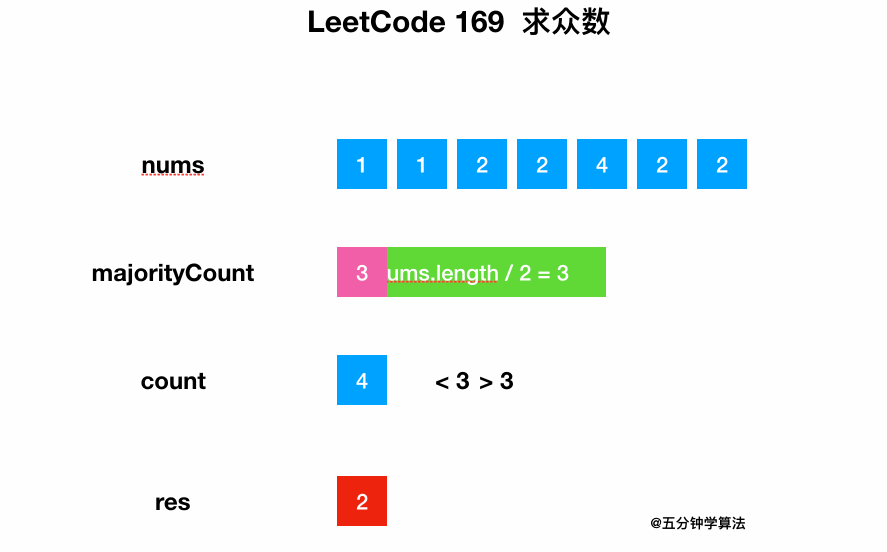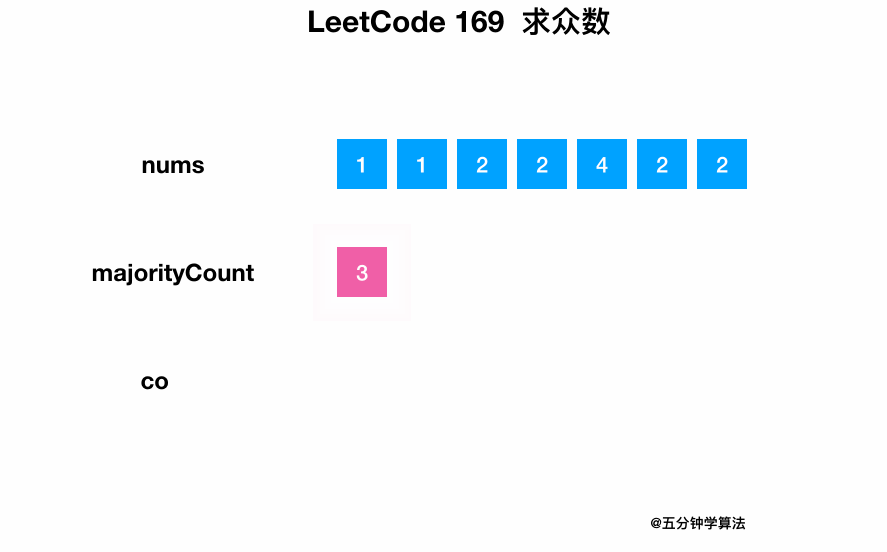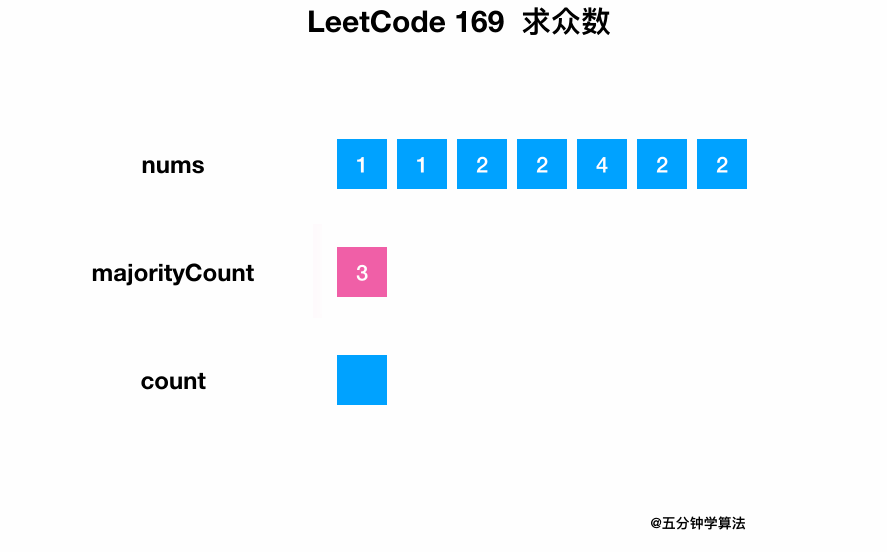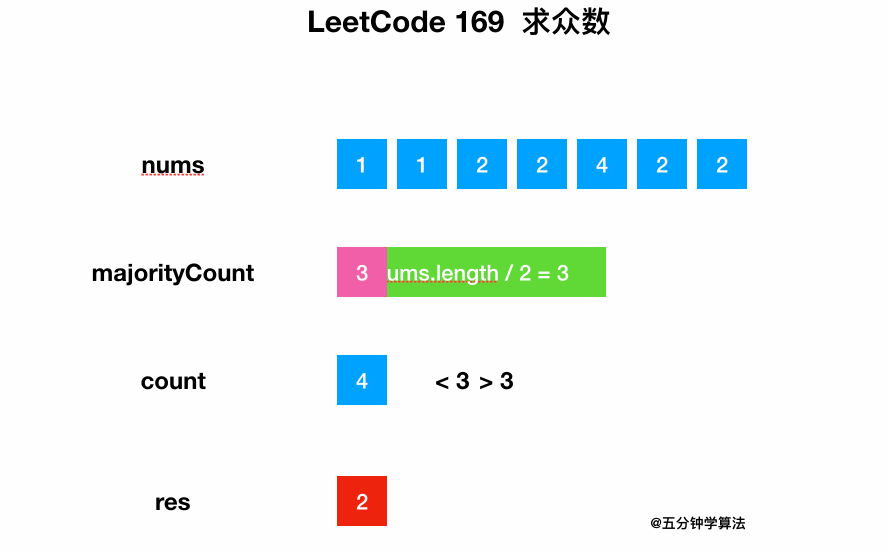
解法一：暴力解法

遍历整个数组，同时统计每个数字出现的次数。

最后将出现次数大于一半的元素返回即可。

动画描述

代码实现

class Solution {
    public int majorityElement(int[] nums) {
        int majorityCount = nums.length/2;

        for (int num : nums) {
            int count = 0;
            for (int elem : nums) {
                if (elem == num) {
                    count += 1;
                }
            }
            if (count > majorityCount) {
                return num;
            }

        }  
    }
}

复杂度分析

时间复杂度：O(n²)

暴力解法包含两重嵌套的 for 循环，每一层 n 次迭代，因此时间复杂度为 O(n²) 。

空间复杂度：O(1)

暴力解法没有分配任何与输入规模成比例的额外的空间，因此空间复杂度为 O(1)。

解法二：哈希表法

这个问题可以视为查找问题，对于查找问题往往可以使用时间复杂度为 O(1) 的 哈希表，通过以空间换时间的方式进行优化。

直接遍历整个 数组 ，将每一个数字（num）与它出现的次数（count）存放在 哈希表 中，同时判断该数字出现次数是否是最大的，动态更新 maxCount，最后输出 maxNum。

动画描述

代码实现

class Solution {
    public int majorityElement(int[] nums) {
    Map<Integer, Integer> map = new HashMap<>();
    // maxNum 表示元素，maxCount 表示元素出现的次数
    int maxNum = 0, maxCount = 0;
    for (int num: nums) {
      int count = map.getOrDefault(num, 0) + 1;
      map.put(num, count);
      if (count > maxCount) {
        maxCount = count;
        maxNum = num;
      }
    }
    return maxNum;
  }
}

复杂度分析

时间复杂度：O(n)

总共有一个循环，里面哈希表的插入是常数时间的，因此时间复杂度为 O(n)。

空间复杂度：O(n)

哈希表占用了额外的空间 O(n)，因此空间复杂度为 O(n)。

解法三：摩尔投票法

再来回顾一下题目：寻找数组中超过一半的数字，这意味着数组中其他数字出现次数的总和都是比不上这个数字出现的次数 。

即如果把 该众数记为 +1 ，把其他数记为 −1 ，将它们全部加起来，和是大于 0 的。

所以可以这样操作：

• 设置两个变量 candidate 和 count，candidate 用来保存数组中遍历到的某个数字，count 表示当前数字的出现次数，一开始 candidate 保存为数组中的第一个数字，count 为 1
• 遍历整个数组
• 如果数字与之前 candidate 保存的数字相同，则 count 加 1
• 如果数字与之前 candidate 保存的数字不同，则 count 减 1
• 如果出现次数 count 变为 0 ，candidate 进行变化，保存为当前遍历的那个数字，并且同时把 count 重置为 1
• 遍历完数组中的所有数字即可得到结果

动画描述

代码实现

class Solution {
    public int majorityElement(int[] nums) {
    int candidate = nums[0], count = 1;
    for (int i = 1; i < nums.length; ++i) {
      if (count == 0) {
        candidate = nums[i];
        count = 1;
      } else if (nums[i] == candidate) {
        count++;
      } else{
        count--;
      }
    }
    return candidate;
  }
}

复杂度分析

时间复杂度：O(n)

总共只有一个循环，因此时间复杂度为 O(n)。

空间复杂度：O(1)

只需要常数级别的额外空间，因此空间复杂度为 O(1)。