1 七桥问题
当时东普鲁士科尼斯堡（今日俄罗斯加里宁格勒）市区跨普列戈利亚河两岸，河中心有两个小岛。小岛与河的两岸有七条桥连接。在所有桥都只能走一遍的前提下，如何才能把这个地方所有的桥都走遍？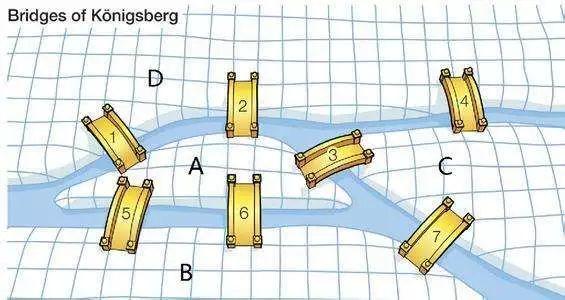
2 问题解决
著名数学家欧拉用 A，B，C，D 四个字母代表陆地，作为图的 4 个顶点，将连接两块陆地的桥作为边，将七桥问题转为数据结构中的图问题。由此得到的图如下：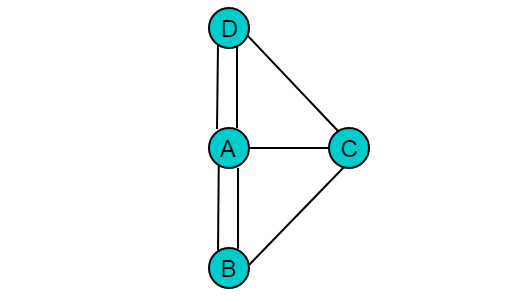
通过将实际问题转为数据结构图论问题，将问题转换为：是否存在每条边只经过一次，且经过所有顶点的回路问题。对于此问题采用欧拉回路的思想去求解。
3 重要概念
通路：图G（v，e）中顶点与边交替出现的序列称为通路，记作：
L = v0，e1，v1，e2，···en，vn。
其中通路 L 中边 e 的数目记作 L 的长度。
回路：在通路中，若v0 = vn，则此通路称为回路。
简单通路：在通路L中，所有的边 e1，e2 ··，en 互不相同。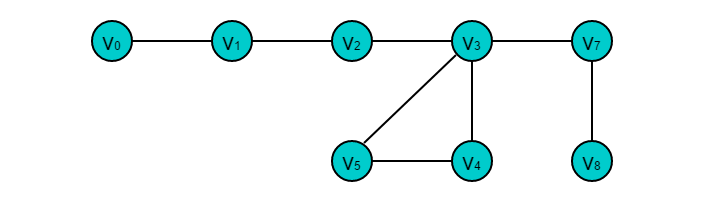
简单回路：在回路中，所有的边e1，e2···，en互不相同。
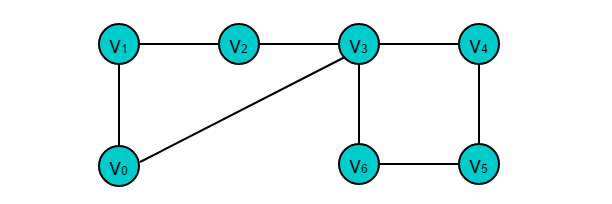
初级通路：所有顶点v0，v1，v2···，vn互不相同的通路
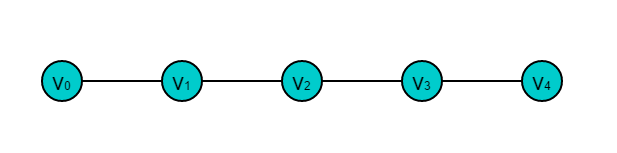
初级回路：所有顶点v0，v1，v2···，vn互不相同的回路
连通图：若图G（v，e）中任意两个顶点都是连通的，则G（v，e）是连通图，否则，G（v，e）为非连通图。
欧拉通路：经过图G（v，e）的每条边一次，且仅仅一次的通路称为欧拉通路，也称为欧拉迹。
欧拉回路：经过图G（v，e）的每条边一次，且仅仅一次的回路称为欧拉回路，也称为欧拉闭迹。
欧拉图：具有欧拉回路的图称为欧拉图。
4 判定
•若图 G 为连通图，且图中又两个顶点的度为奇数，则图 G 具有欧拉通路，且以两个奇度顶点为端点。•若图 G 为连通图，且没有奇度顶点，则图 G 具有欧拉回路。•若图 G 为连通图，且有 2k 个奇度顶点，则图需要用 k 笔画成，且至少需要k笔才能画成。
5 例题分析
5.1 七桥问题解决
由图 2.1 可以看出，七桥问题的图 G 中存在 4 个奇度顶点，则此图需要 2 笔才能画成，不存在欧拉回路和欧拉通路。因此若要遍历图，必然要经过重复的边。
5.2 遍历房间问题
如下图所示的一幢房屋的平面图，由前门进入到达客厅，由客厅可以通向四个卧室，请问是否能够从前门进入，通过所有的门，走遍客厅和 4 个卧室，最后从后门走出。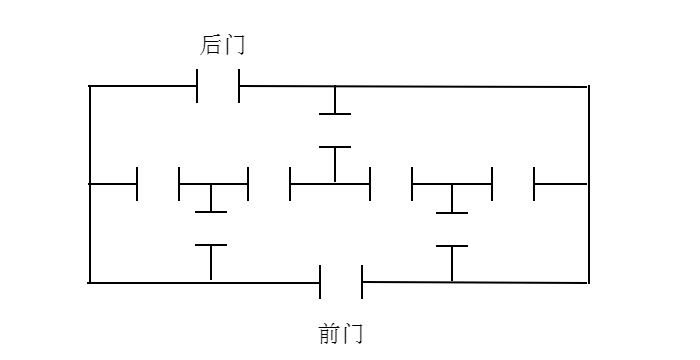
问题分析：将 5 个房间以及前门后门外的地方均作为顶点，有门相通则表示顶点邻接，得到图 G，如下图所示：
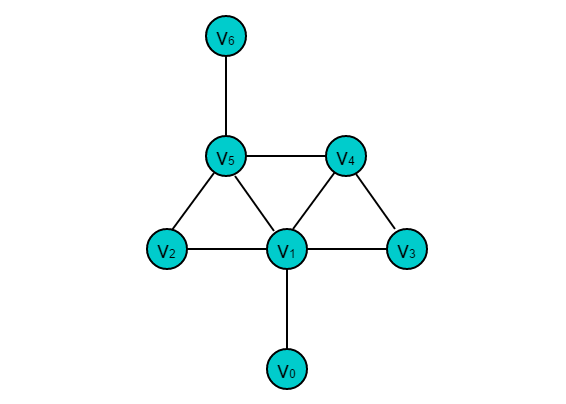图 G 中，奇度顶点的数目是 4，故图 G 不是欧拉通路，因此答案是否定的。
5.3 一笔画
一笔画问题是欧拉图的典型应用。例如如下图形，是否可以用一笔画成。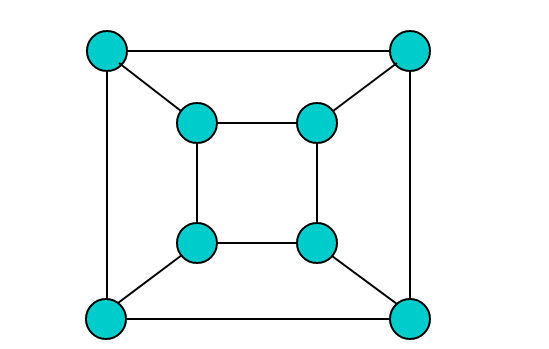
观察图中的奇度顶点共有 8 个，因此图需要 4 笔才能画成。
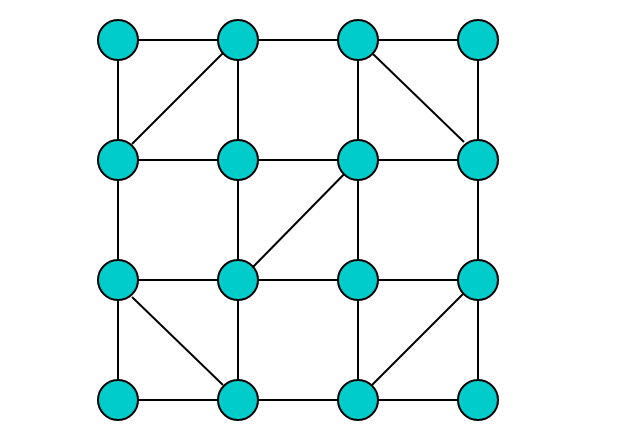观察图中的奇度顶点共有 2 个，则此图可以 1 笔画成，且图存在欧拉通路，通路的端点即为奇点度数为 5 的顶点。
END
推荐阅读：
欢迎长按下图关注公众号五分钟学算法，一起学算法。
来和程序员小吴一起学算法
