LeetCode 二叉树问题小总结

导言

LeetCode 上面的二叉树问题一般可以看成是简单的深度优先搜索问题，一般的实现方式是使用递归，也会有非递归的实现方法，这边文章主要介绍一下解决二叉树问题的几个常规方法和思路，然后会给一个从递归转换到非递归的小技巧。

两个通用方法和思路

拿到一道二叉树的问题，多半是需要你遍历这个树，只不过是在遍历的过程中，不同的题目要求你做的计算不一样。

这里有两个遍历方法，自顶向下的递归遍历，以及自底向上的分治。

两种方法都用到了递归，在代码实现上面，差别不是特别大，但是思路却截然相反，我们拿树的中序遍历这道题目来作为示例。

事实上，在 LeetCode 以及面试过程中，对二叉树的遍历考察的非常多，所以，请务必理解二叉树的前、中、后序三种遍历方式。

花几分钟借助下面三个动画彻底理解一下二叉树遍历的过程吧。

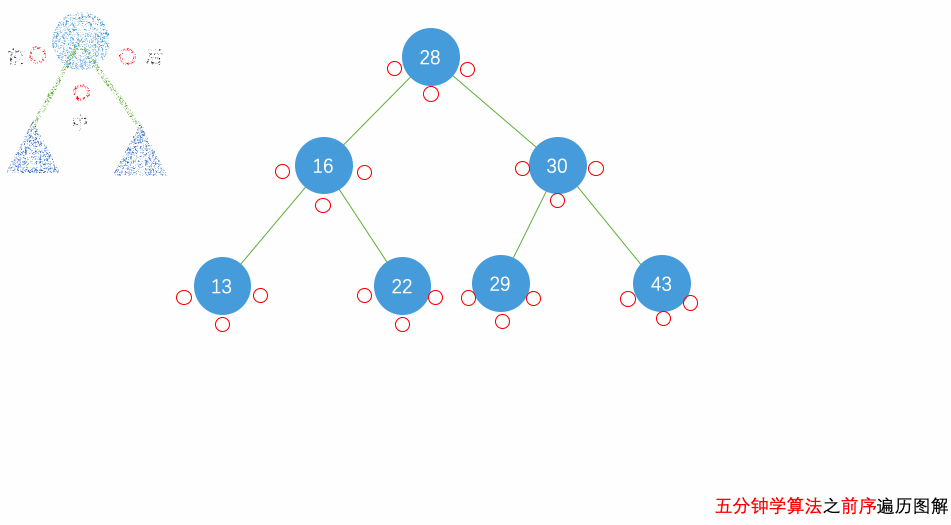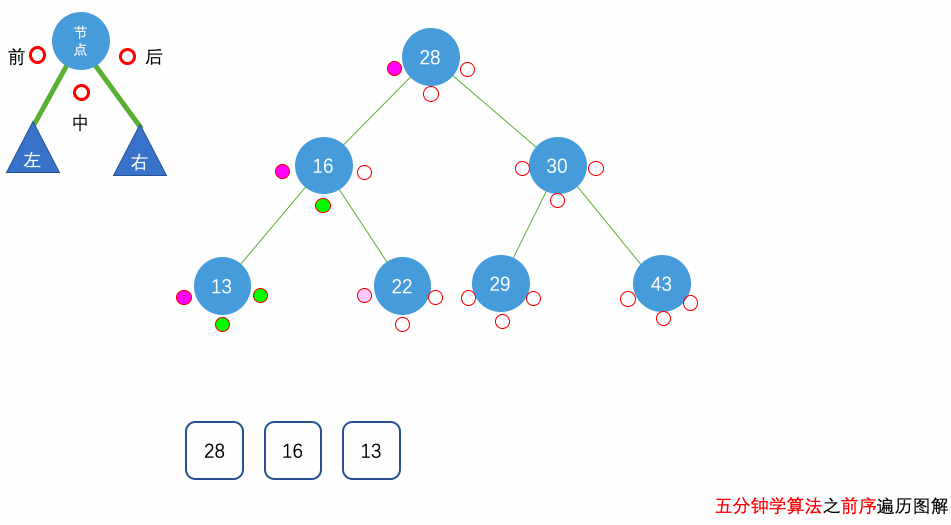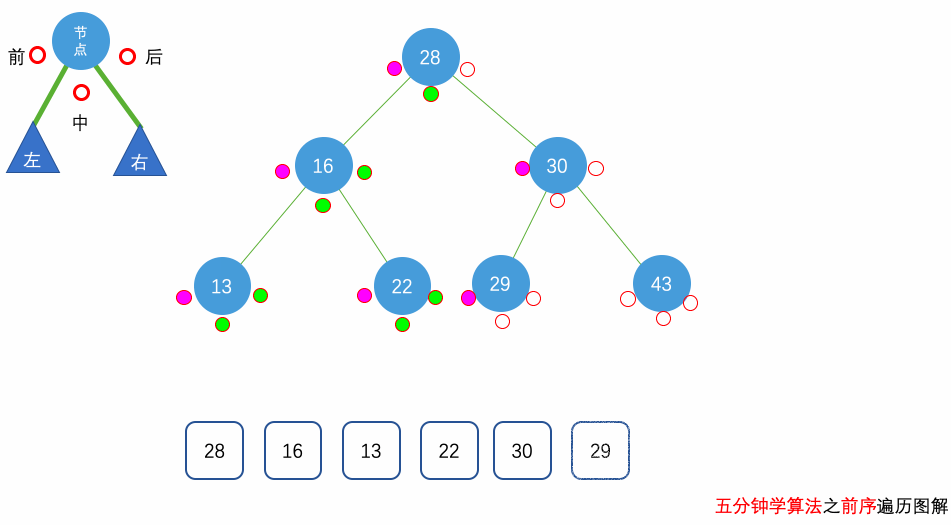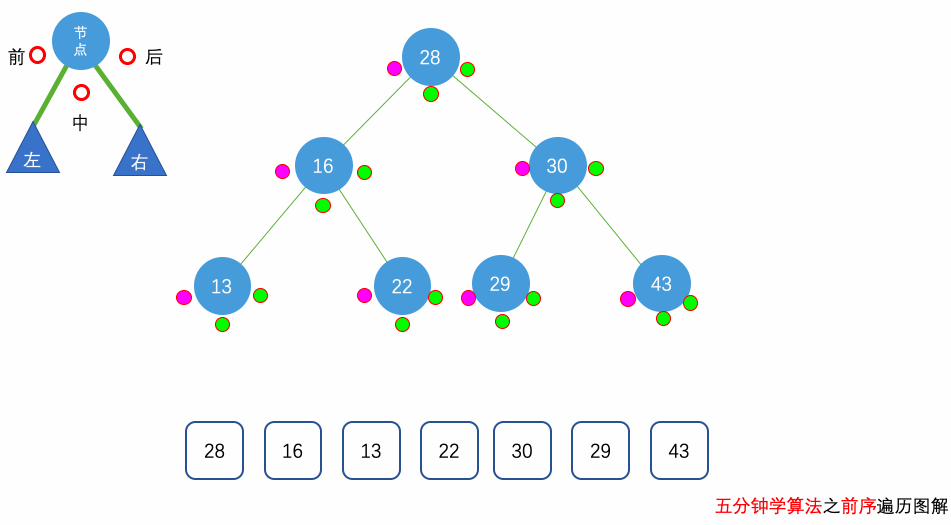
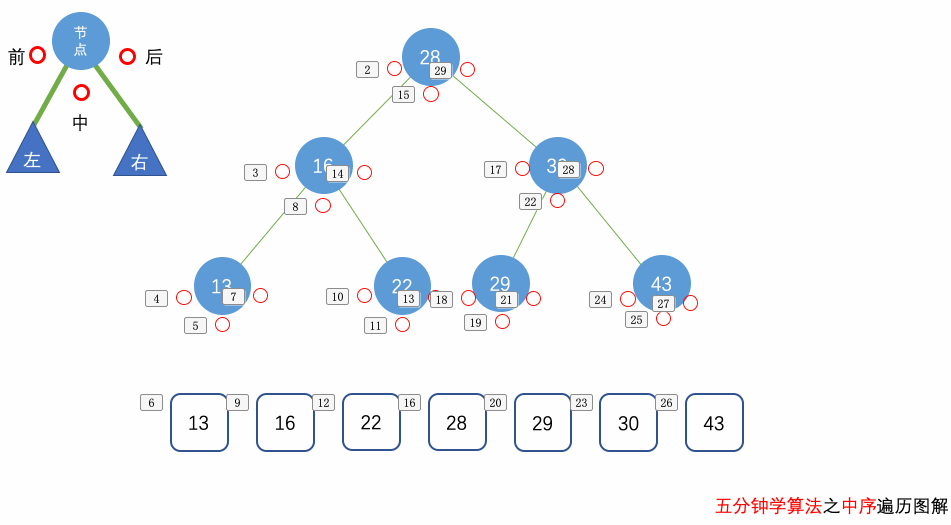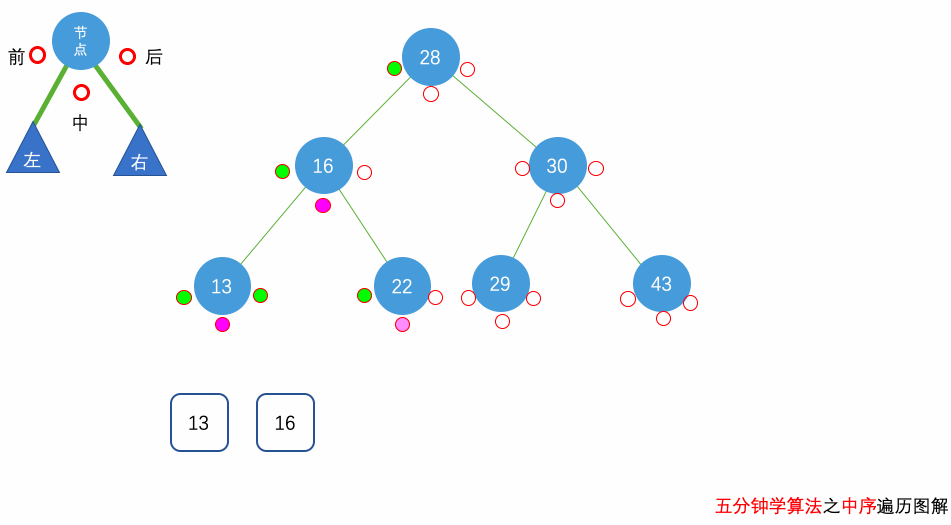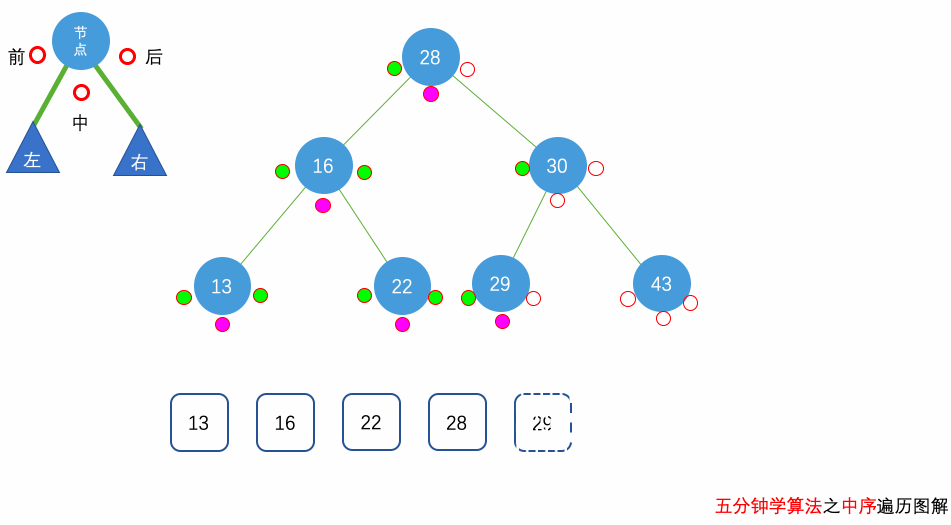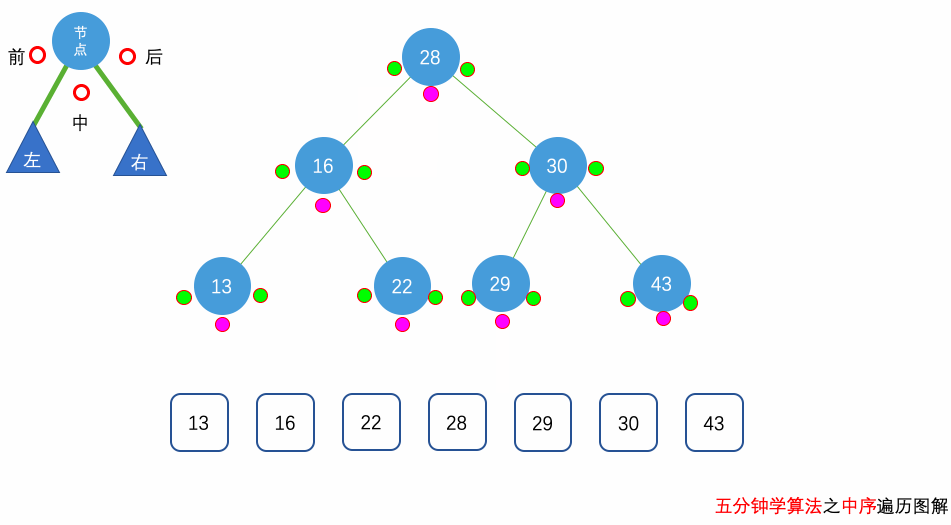
自顶向下的递归遍历

public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer> result = new ArrayList<>();
    if (root == null) {
        return result;
    }

    helper(root, result);

    return result;
}

private void helper(TreeNode root, List<Integer> result) {
    if (root == null) {
        return;
    }

    helper(root.left, result);
    result.add(root.val);
    helper(root.right, result);
}

代码非常的简短，上面代码的重心全放在了 helper 函数上，这个函数没有返回值，它做的事情也非常的简单，就是去到对应的树节点，然后把节点的值加到 result 中。

这里我们要求的是树的 中序遍历，因此，我们要先去到当前树节点的左边，把左边所有的节点的值放到 result 中，才会继续放当前树节点，放完当前树节点的值后，我们会去到右边进行同样的操作。

对于这种实现方法其实有点类似于循环遍历，只不过循环遍历只作用于数组还有链表这样的线性结构，对于树的话，这里我们采用了递归的方式去遍历，你可以想象成一个小人在一棵树上面游走，他的目的是按顺序去记录树的节点值。

自底向上的分治

public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer> result = new ArrayList<>();

    if (root == null) {
        return result;
    }

    result.addAll(inorderTraversal(root.left));
    result.add(root.val);
    result.addAll(inorderTraversal(root.right));

    return result;
}

同一个问题，再来看看我们之前提到的另外一种思路实现。

这里我们也使用了递归，但是这次的递归函数是有返回值的，而且你也可以看到的是，我们没有将保存结果的 list 传入函数。

正因为是自底向上，所以对于一个树节点来说，它这里会知道它子节点的返回值，也就是子节点的记录结果，在它这里会把左右子节点的结果，和它自己本身的结果汇总，然后将汇总的结果返回给上一层节点。

和之前的递归遍历的思路相比的话，代码实现上面的区别可能就是，是将 result list 放在参数中，还是放在返回值中，但是思考方向是截然相反的。

这里就不好用之前的 “小人游走” 来解释了。

更好的解释方式是公司职位，这里你可以想象每个树节点就是企业里面的一个人，或者说是一个职位，最上面的 root 节点就是企业的 CEO，往下是副总裁，然后再往下是总监，总监往下是经理，。。。在副总裁这里，他会向他下面的两个总监要结果，在他这里把两个总监返回的结果汇总，然后上报给 CEO，他不会去关注经理的结果，底层员工的结果，在他这里，只关心下一层和上一层。

这两种方法没有好坏之分，有的题目使用自顶向下递归遍历的方式会比较直接一点，比如求最大最小值，有些题目则使用自底向上分治的方式会比较好一些，比如说 subtree 的问题。对于不同的题目，我们需要选择不同的方法，但是思考方式可以考虑从这两个方向去思考。

一般来说，二叉树问题的时间复杂度都是 O(n) ，这个时间复杂的怎么理解呢？你可以看成是在每个树节点上的操作的时间复杂度是 O(1)，但是要遍历所有的节点，因此 O(1) * n = O(n)。

递归转非递归

对于树的问题，我们也可以使用非递归的方式求解，其实任何一个递归的解法，都可以转换为非递归，而且就性能和稳定性来说的话，非递归的方式要比递归来的好。

但是问题是，非递归代码不是那么好写，通常来说递归的解法会简洁不少，因此在面试中，面试官通常会让写递归。

但是，有些时候，面对一个简单的问题，有些面试官会让你写出非递归的解法，比如上面的中序遍历的例子，相比于递归的简洁一致，非递归的实现可能每个人写出来都会略有不同，我记得我第一次试着把递归写成非递归是非常痛苦的，完全没有头绪。

我这里给出了一个递归转非递归的通用方法，不仅仅适用于树的问题，对于任何的递归问题都适用，这个方法也是我在 LeetCode 的 discuss 中看到的，还是拿上面中序遍历作为例子，之前我们的代码实现：

public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer> result = new ArrayList<>();
    if (root == null) {
        return result;
    }

    helper(root, result);

    return result;
}

private void helper(TreeNode root, List<Integer> result) {
    if (root == null) {
        return;
    }

    helper(root.left, result); // line 0
    result.add(root.val);      // line 1
    helper(root.right, result);// line 2
}

你可以看到，我在 helper 函数最后 3 行代码标上了序号，后面的非递归实现的程序中会用到，这里我们主要是要实现 helper 函数中的东西。

非递归代码如下：

public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer> result = new ArrayList<>();
    if (root == null) {
        return result;
    }

    Stack<Integer> systemStack = new Stack<>(); // 表示函数进度
    Stack<TreeNode> paramStack = new Stack<>(); // 表示函数输入参数

    systemStack.push(0);
    paramStack.push(root);

    while (!systemStack.isEmpty()) {
        int curLine = systemStack.pop();
        TreeNode curParam = paramStack.peek();

        // 提前将当前进度后移，因为后面可能会有其他函数入栈
        systemStack.push(curLine + 1);

        if (curLine == 0) {
            if (curParam.left != null) {
                systemStack.push(0);
                paramStack.push(curParam.left);                    
            }
        } else if (curLine == 1) {
            result.add(curParam.val);
        } else if (curLine == 2) {
            if (curParam.right != null) {
                systemStack.push(0);
                paramStack.push(curParam.right);
            }
        } else {
            systemStack.pop();
            paramStack.pop();
        }
    }

    return result;
}

一般来说，用非递归写递归，都需要用到一个数据结构-栈。

这个好解释，递归的解法是利用了系统中提供的函数栈，非递归我们需要手动创建这么一个数据结构，但是你可能会问的是，这里为什么要用到两个栈？

你可以这样认为，一个栈用来表示函数的运行进度，里面的元素表示此时该函数运行到了第几行代码，另一个栈用来记录函数的传入参数，当然你也可以把这两个栈合成一个栈，里面装的是封装好的对象。

这里为了解释起来清晰直观，就用两个栈。

首先，根据之前的递归解法，我们最开始是把 root 传入 helper 函数，因此这时我们也把 root 加入函数栈，另外一个表示函数进度的栈往里面添加 0，表示当前函数运行到了第 0 行，然后就是 while 循环里面的东西，while 循环一开始我们就获取当前函数的输入参数和进度，然后根据函数的进度去看需要执行哪一段代码，因为有的代码会继续往栈里面添加函数，因此，我们需要提前把函数进度往后移动，你可以对应之前的递归的代码和我标的序号，你可以看到，整个 if-else if…else 部分就表示了之前的递归函数中的代码，只不过这里我们需要根据函数的进度去判断它要执行哪一行。

使用这种方法后，递归转非递归只需要往上套就行，不需要单独分析。