大家好,我是吴师兄。
今天继续分享 LeetCode 上的骚评论、骚操作。
这个评论来源于 剑指 Offer 14 : 剪绳子。
这又是一个面向测试用例编程的代码。
提交看看结果。

空间、时间都是 O(1) 级别,打表法 YYDS,比赛必备的神器,想在比赛中得奖,还真得用这种技巧。
如果作为练习来说,我们还是得掌握正统的解法,因为,在面试过程中,打表法肯定是被禁止的。
想一想,面试官问你这道题目怎么思考。
你闭着眼睛开始说答案:0, 0, 1, 2, 4, 6, 9, 12, 18, 27, 36, 54, 81 。。。

对于这道题目来说,贪心算法的效率是远远高于动态规划的,一个是 O(n),一个则是 O(n^2)。
但是,动态规划更好理解,也更加容易和面试官拉扯,建议掌握。
那先来看一下题目描述。

我们假设绳子的长度为 10。

先来剪一下,假设一开始剪下来的长度为 1,那么左边绳子的长度为 1,右边绳子的长度为 9,它们的乘积为 1 * 9 = 9。
对于一段一开始长度为 10 的绳子而言,9 是小于 10 的,因此剪下长度为 1 的绳子是无法增大乘积的,更一般的来说,1 和任何数相乘都是那个数本身,因此对于任意长度的绳子来说都不应该剪长度为 1 的绳子下来。
数学证明: n > ( n - 1) * 1。
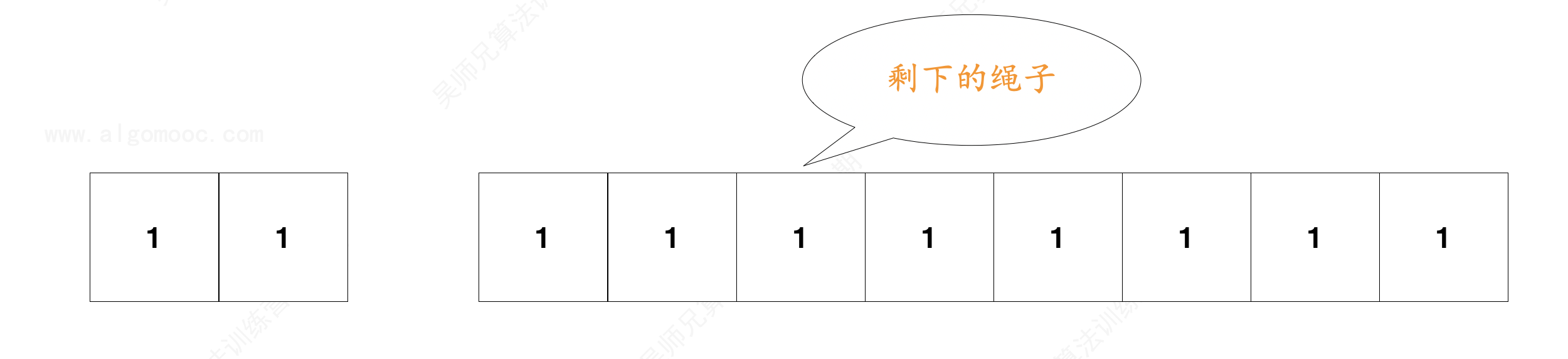
所以,每次剪绳子的操作都是剪至少长度为 2 的绳子的操作。
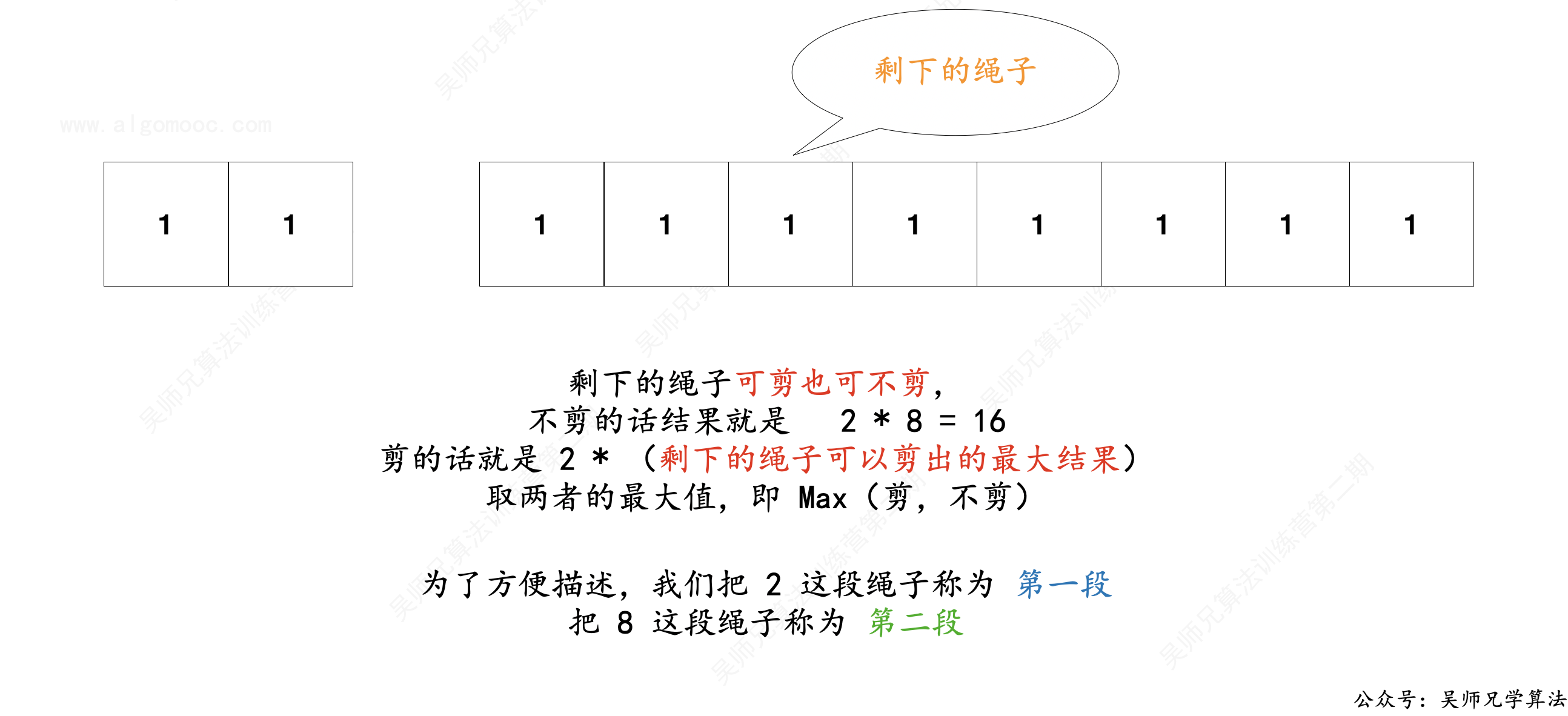
当剪下一段长度为 2 的绳子时,剩下的绳子长度为 8。
那么对于长度为 8 的这段绳子来说,它有两个选择,剪或者不剪。
- 不剪,乘积结果为
2 * 8 = 16; - 剪,怎么剪?
对于这两个选择,我们无法第一时间做出决定,因为目前还不知道剪的情况下能否出现大于 16 的结果。

所以,接下来的操作就是去剪第二段绳子。
怎么剪呢?
和剪长度为 10 的那段绳子一样的思路。
剪完之后,第二段绳子也被划分两块区域,a 和 b。
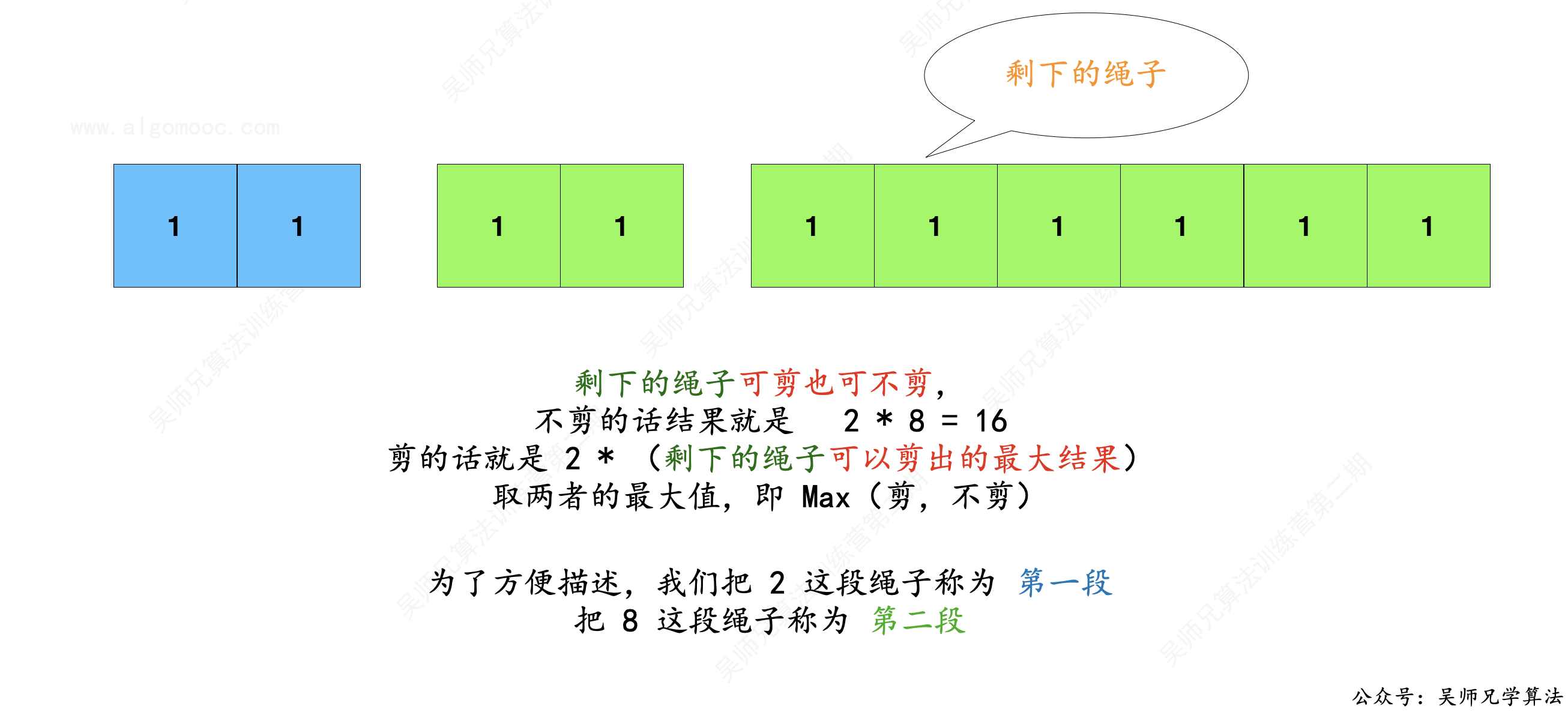
通过剪长度为 10 的绳子与长度为 8 的绳子的操作,我们可以发现:我们在不停的去剪相对的那根 第二段 的绳子,直到剪无可剪为止。
此时我们考虑第二段的情况时,第一段绳子的长度为 2,而事实上,第一段绳子可取的范围为 [ 2,i)。
此时,假设当下绳子的长度为 i。
长度为 n 的绳子剪掉后的最大乘积与求绳子长度为 n - 1 、 n - 2 、 n - 3 的最大乘积求法一样。
假设剪的绳子那段称为 第一段,剪剩下的那段绳子称为 第二段,那么第一段的范围为 [2,i),第二段可以剪或者不剪,假设 dp[i] 表示长度为 i 的绳子剪成 m 段后的最大乘积,那么,不剪总长度乘积为 j * ( i - j),剪的话长度乘积为 j * dp[ i - j ],取两者的最大值,即 Max ( j * ( i - j) , j * dp[ i - j] )。
状态转移方程:dp[i] = Max(dp[i], Max(j * (i - j), j * dp[i - j]))
思考到这里,代码也就自然而然的出来了。
// 登录 AlgoMooc 官网获取更多算法图解
// https://www.algomooc.com
// 作者:程序员吴师兄
// 代码有看不懂的地方一定要私聊咨询吴师兄呀
class Solution {
public int cuttingRope(int n) {
// 长度为 1 的绳子没法剪了
if ( n <= 1 ) return 1;
// 用一个名为 dp 的数组来记录从 0 到 n 长度的绳子剪掉后的最大乘积
// 默认都是 0
int[] dp = new int[n + 1];
// 由于绳子必须被剪,所以长度为 2 的绳子只有剪成 1 和 1 的两段,乘积结果为 1
dp[2] = 1;
// 长度大于等于 3 的绳子才开始进入我们的讨论范围
// 从长度为 3 的绳子开始考虑,讨论它的最大乘积是多少,并不断的延伸绳子的长度
for(int i = 3; i < n + 1; i++){
// 对于长度为 i 的绳子,它可以分为两个区间 j 和 i - j
// j 的范围由 2 开始,因为剪长度为 1 的绳子无法扩大乘积的值
// j 的范围可以延伸至 i - 1
for(int j = 2; j < i; j++){
// 不剪总长度乘积为 j * ( i - j)
// 剪的话长度乘积为 j * dp[ i - j ]
// 取两者的最大值,即 Max ( j * ( i - j) , j * dp[ i - j] )
// 那么此时 dp[i] 的值取 i 不剪的值( dp[i]) 和剪的值 Math.max(j * (i - j), j * dp[i - j]) 这两者的最大值
// 比如一开始 i = 3 , j = 2
// dp[3] = Math.max( 0 ,Math.max ( 2 * 1, 2 * dp[1])
// = Math.max( 0 ,Math.max ( 2, 2))
// = 2
dp[i] = Math.max(dp[i], Math.max(j * (i - j), j * dp[i - j]));
}
}
return dp[n];
}
}




