懵逼树上懵逼果：学习二分搜索树

数组、栈、队列、链表都是线性结构，树则是另外一种极其重要的数据结构。

树的种类有很多种，我们先从简单的 二分搜索树 开始树的学习。

二分查找法

二分查找法定义

是一种在有序数组中查找某一特定元素的搜索算法。

搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；

如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。

如果在某一步骤数组为空，则代表找不到。

这种搜索算法每一次比较都使搜索范围缩小一半。

动画演示

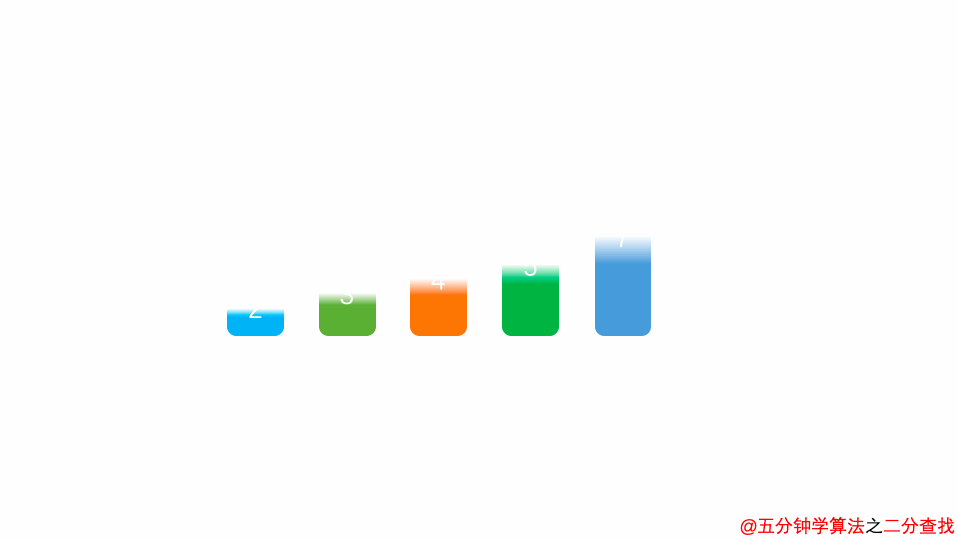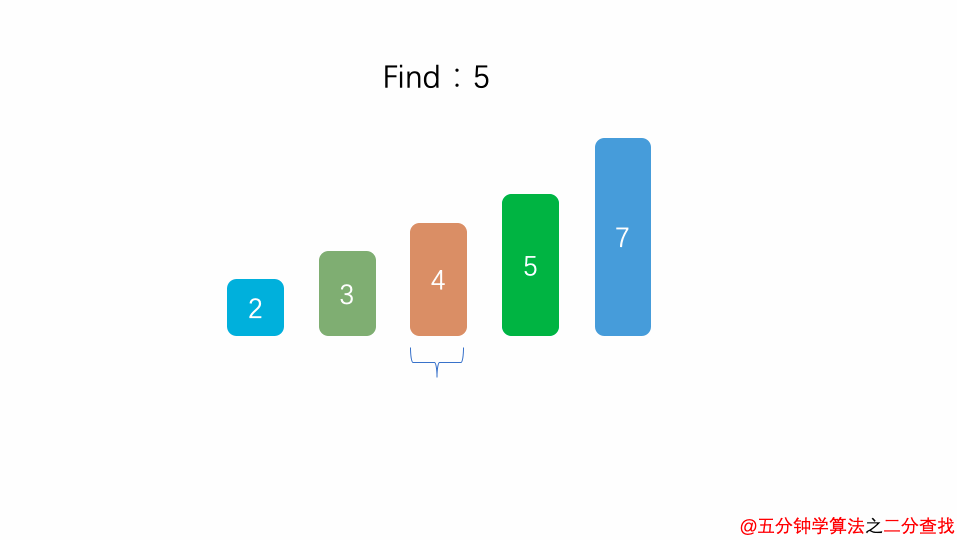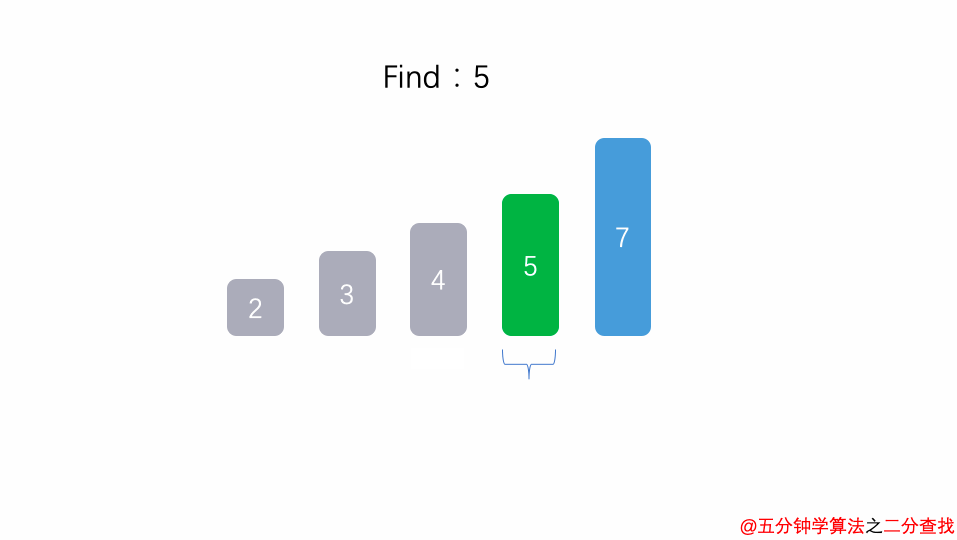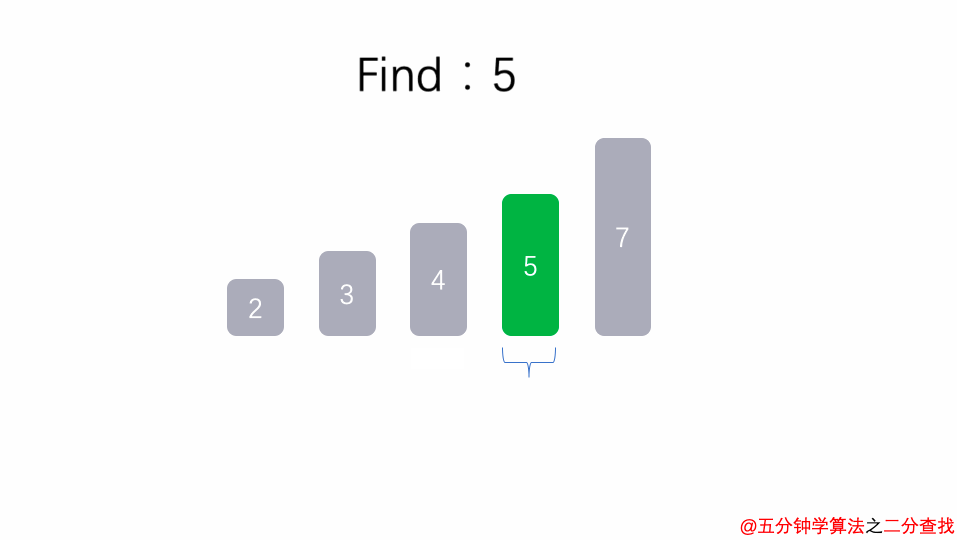
动画说明

注意：二分查找的前提是数列必须是有序的。

• 目标是搜索数字 5

• 首先，检查有序数列中心的数字，这里查找到时数字 4

• 4 与 将要搜索的数字 5 进行比较，由于 4 小于 5，图中可以发现 5 在 4 的右边

• 这时，就不需要观察 4 左边的数字了，置灰删除掉

• 检查剩余有序数列中心的数字，这时是 5

• 找到了这个数字

二叉查找树（Binary Search Tree）基础

二叉查找树也可叫做二分查找树。

它不仅可以查找数据，还可以高效地插入、删除数据。

特点：每个节点的key值大于左子节点，小于右子节点。

注意它不一定是完全的二叉树。

class Node {   E e;   Node left;  // 左孩子   Node right; // 右孩子 }

二叉查找树有两个属性：

• 所有节点都比左子树中的节点大

• 所有节点都小于右子树中的节点

通过这两个属性，可以推断出以下结论：

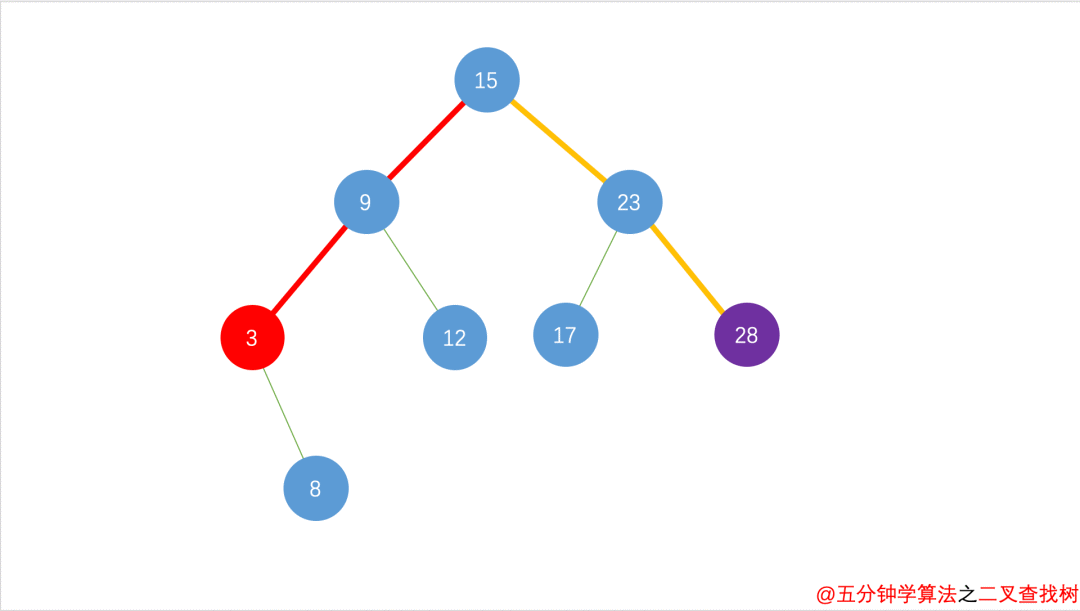
• 二叉查找树最小的节点位于最顶端节点的最左边子树行的末尾（如图数字 3 ）

• 二叉查找树的最大节点位于最顶端节点的最右边的子树行的末尾（如图数字 28 ）

通过以下方式的进行添加元素与删除元素的操作，可以保留二叉查找树的完整性。

我们通过两组添加元素，三组删除元素，一组查找元素的操作来理解二叉查找树的属性性质。

添加元素操作

核心思想:从根节点开始找插入的位置，满足二叉搜索树的特性，比左子节点大，比右子节点小.

步骤：

• 从根节点开始，先比较当前节点，如果当前节点为null那么就插入到这个节点。

• 如果上面的节点不是null，那么和当前节点比较，如果小于节点就往左子树放，如果大于节点就往右子树放。

• 然后分别对左子树或者右子树递归的递归进行如上 1 、 2 步骤的操作

添加元素 1

• 从二叉查找树的最顶端节点开始，去找到附加节点的正确位置

• 由于 1 < 15 ， 向左走

• 1 < 9 ，继续向左走

• 1 < 3，继续向左走，但因为没有节点在其后序前方，因此将它作为一个新节点进行添加

添加元素 4

• 同样的从二叉查找树的最顶端节点开始，去找到附加节点的正确位置

• 由于 4 < 15 ， 向左走

• 4 < 9 ，继续向左走

• 4 > 3，向右走

• 4 < 8，向左走，但因为没有节点在其后序前方，因此将它作为一个新节点进行添加

代码实现

删除元素操作

步骤：

• 找到左子树中找左子树中所有节点的最大的节点

• 将这个节点赋值到删除节点的位置

删除元素 28

• 该节点没有子类，直接删除

删除元素 8

• 该节点有1个子类

• 目标节点被删除，将子节点移动到已删除节点的位置

删除元素 9

• 该节点有2个子类

• 目标节点被删除，从删除节点的左子树中找到最大的节点，将其移到到删除的节点的位置

代码实现

查找元素操作

查找元素 12

• 同样的，从二叉查找树的最顶端节点开始搜索

• 12 < 15 ，向左走

• 12 > 4 ，向右走

• 找到 12

代码实现

可以看出，使用二叉查找树可以实现高效搜索。

但是如果树接近形成直线，那么搜索效率将极其差，变成了线性搜索。

因此二叉查找树就需要进行改进为平衡二叉树，比较常见的 Balanced Binary Tree有：

• 红黑树

• tree

• AVL tree

• Splay tree

• Treap

二分搜索树的遍历

遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。二叉树的遍历有三种：

• 前序遍历(Preorder Traversal)：先访问当前节点，再依次递归访问左右子树

• 中序遍历(Inorder Traversal)：先递归访问左子树，再访问自身，再递归访问右子树

• 后序遍历(Postorder Traversal)：先递归访问左右子树，最后再访问当前节点。

前序遍历

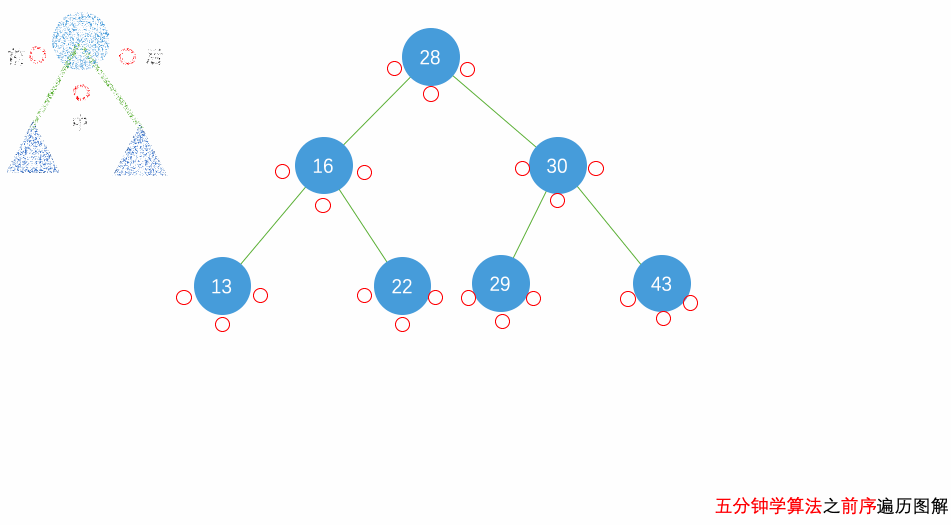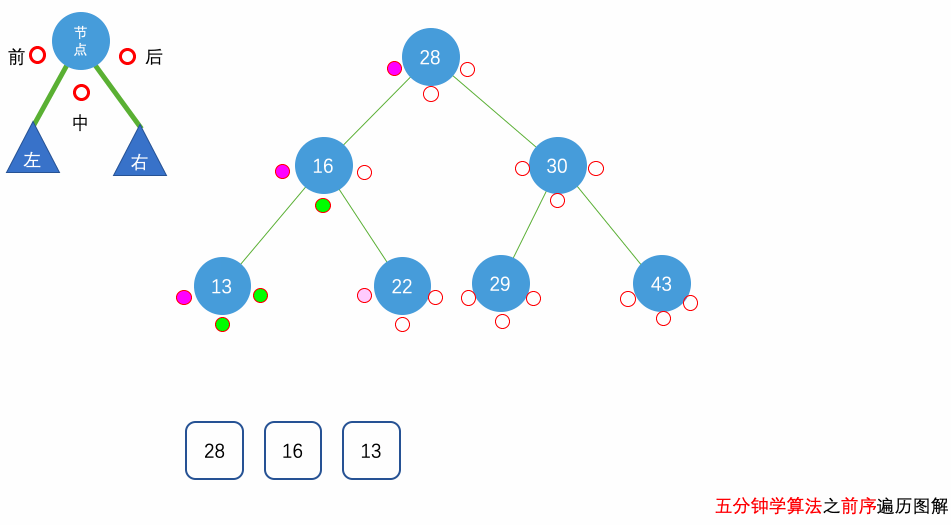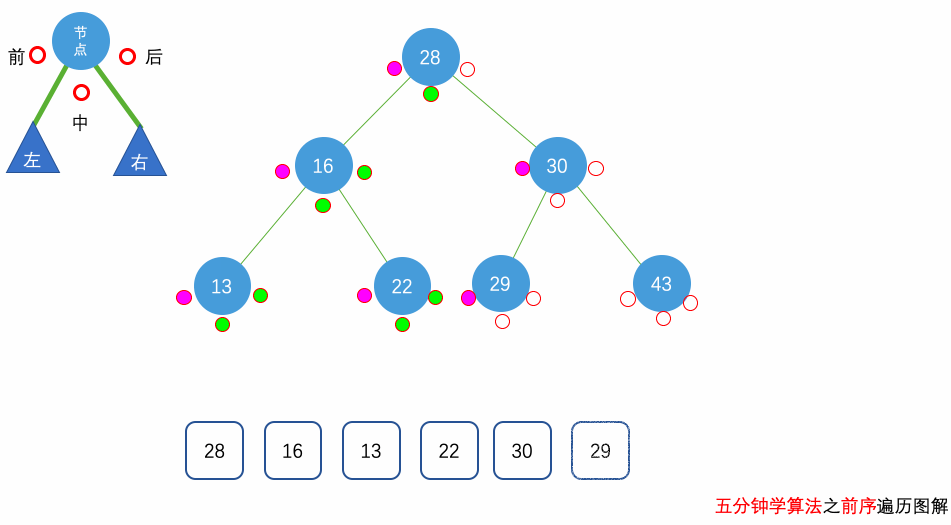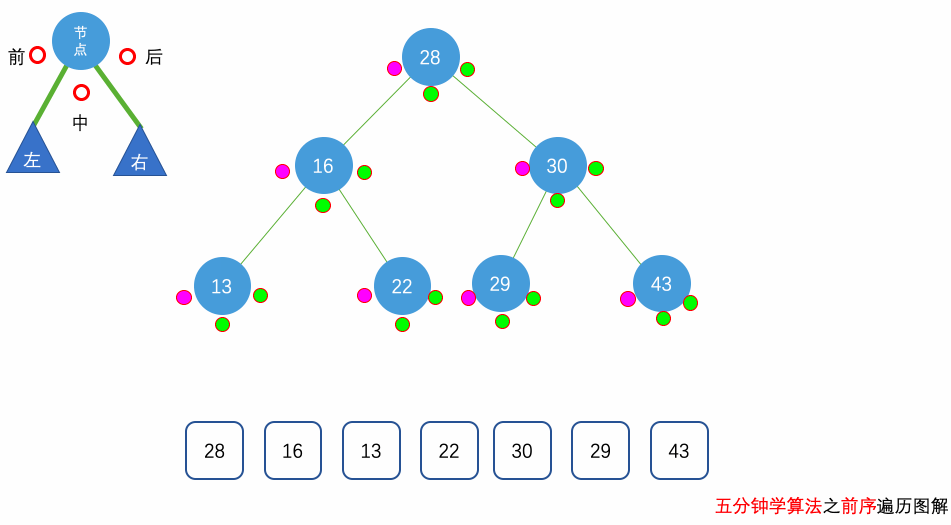
中序遍历

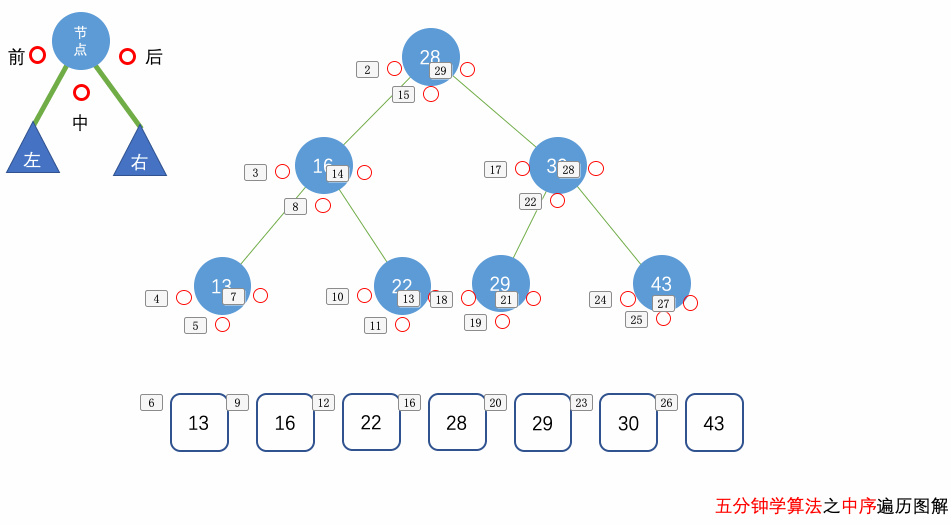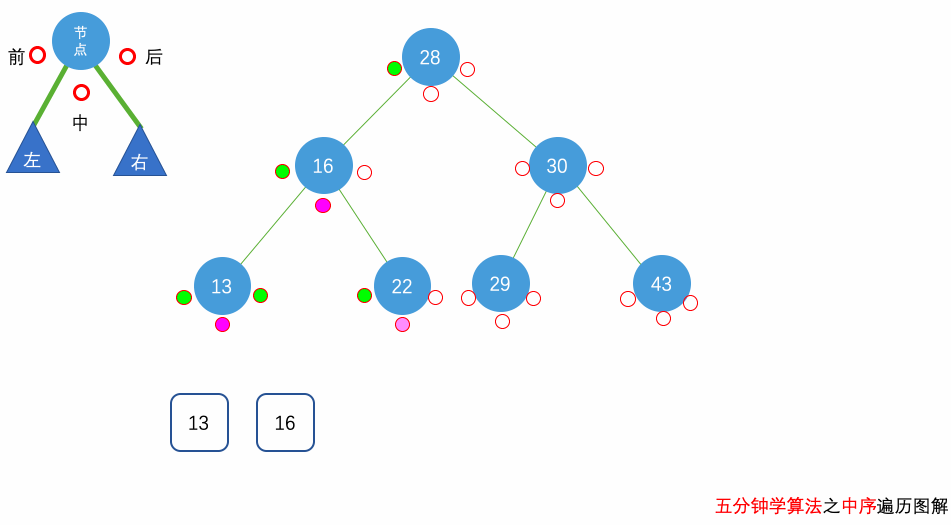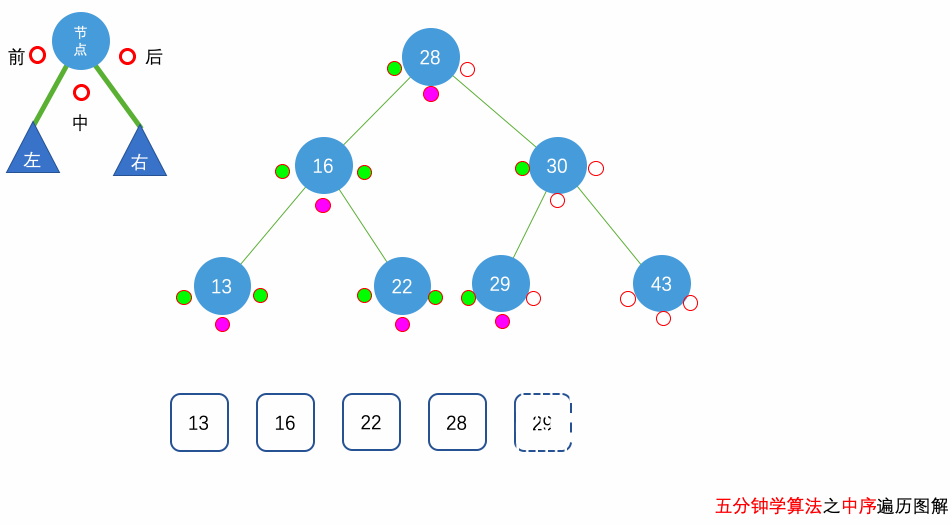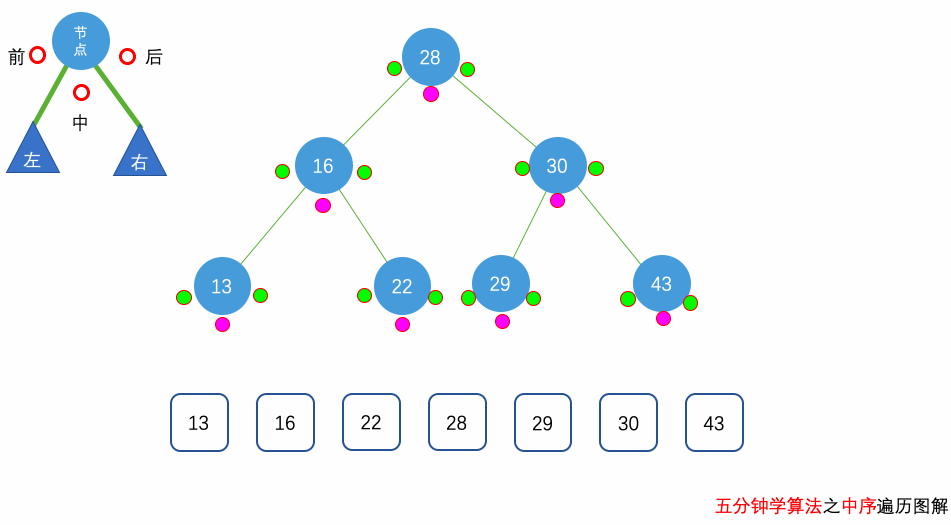
后序遍历

具体分析可查看博主的前面的文章《【图解数据结构】 一文弄懂二叉树三种遍历》。