拜托，面试官别问我「布隆」了（修订补充版）

前言

在之前的拜托，面试官别问我「布隆」了一文中，很多小伙伴留言说并不能看出布隆过滤器有比位图更方便，今天的文章就补充更详细一点。

题目描述

一个网站有 100 亿 url 存在一个黑名单中，每条 url 平均 64 字节。这个黑名单要怎么存？若此时随便输入一个 url，你如何快速判断该 url 是否在这个黑名单中？

题目解析

这是一道经常在面试中出现的算法题。凭借着题目极其容易描述，电面的时候也出现过。

不考虑细节的话，此题就是一个简单的查找问题。对于查找问题而言，使用散列表来处理往往是一种效率比较高的方案。

但是，如果你在面试中回答使用散列表，接下来面试官肯定会问你：然后呢？如果你不能回答个所以然，面试官就会面无表情的通知你：今天的面试到此结束，我们会在一周内给你答复。

为什么不能用散列表

100 亿是一个很大的数量级，这里每条 url 平均 64 字节，全部存储的话需要 640G 的内存空间。又因为使用了散列表这种数据结构，而散列表是会出现散列冲突的。为了让散列表维持较小的装载因子，避免出现过多的散列冲突，需要使用链表法来处理，这里就要存储链表指针。因此最后的内存空间可能超过 1000G 了。

只是存储个 url 就需要 1000G 的空间，老板肯定不能忍！

位图（BitMap）

这个时候就需要拓展一下思路。首先，先来考虑一个类似但更简单的问题：现在有一个非常庞大的数据，比如有 1 千万个整数，并且整数的范围在 1 到 1 亿之间。那么如何快速查找某个整数是否在这 1 千万个整数中呢？

需要判断该数是否存在，也就是说这个数存在两种状态：存在（ True ）或者不存在（False）。

因此这里可以使用一个存储了状态的数组来处理。这个数组特点是大小为 1 亿，并且数据类型为布尔类型（ True 或者 False ）。然后将这 1 千万个整数作为数组下标，将对应的数组值设置成 True，比如，整数 233 对应下标为 233 的数组值设置为 True，也就是 array[ 233 ] = True。

这种操作就是位图法：就是用每一位来存放某种状态，适用于大规模数据，但数据状态又不是很多的情况。

另外，位图法有一个优势就是空间不随集合内元素个数的增加而增加。它的存储空间计算方式是找到所有元素里面最大的元素（假设为 N ），因此所占空间为：

拜托，面试官别问我「布隆」了（修订补充版）

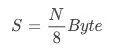
因此，当 N 为 1 亿的时候需要 12MB 的存储空间。当 N 为 10 亿的时候需要 120MB 的存储空间了。当 N 的数量大到一定量级的时候，比如 N 为 2^64 这个海量级别的时候，需要消耗 2048PB 的存储空间，这个量级的BitMap，目前硬件上是支持不了的。

也就是说：位图法的所占空间随集合内最大元素的增大而增大。这就会带来一个问题，如果查找的元素数量少但其中某个元素的值很大，比如数字范围是 1 到 1000 亿，那消耗的空间不容乐观。

这个就是位图的一个不容忽视的缺点：空间复杂度随集合内最大元素增大而线性增大。对于开头的题目而言，使用位图进行处理，实际上内存消耗也是不少的。

因此，出于性能和内存占用的考虑，在这里使用布隆过滤器才是最好的解决方案：布隆过滤器是对位图的一种改进。

布隆过滤器

布隆过滤器（英语：Bloom Filter）是 1970 年由 Burton Bloom 提出的。

它实际上是一个很长的二进制矢量和一系列随机映射函数。

它可以用来判断一个元素是否在一个集合中。它的优势是只需要占用很小的内存空间以及有着高效的查询效率。

对于布隆过滤器而言，它的本质是一个位数组：位数组就是数组的每个元素都只占用 1 bit ，并且每个元素只能是 0 或者 1。

一开始，布隆过滤器的位数组所有位都初始化为 0。比如，数组长度为 m ，那么将长度为 m 个位数组的所有的位都初始化为 0。

0	0	0	0	0	0	0	0	0	0
0	0	1	。	。	。	。	。	m-2	m-1

在数组中的每一位都是二进制位。

布隆过滤器除了一个位数组，还有 K 个哈希函数。当一个元素加入布隆过滤器中的时候，会进行如下操作：

•使用 K 个哈希函数对元素值进行 K 次计算，得到 K 个哈希值。•根据得到的哈希值，在位数组中把对应下标的值置为 1。

拜托，面试官别问我「布隆」了（修订补充版）

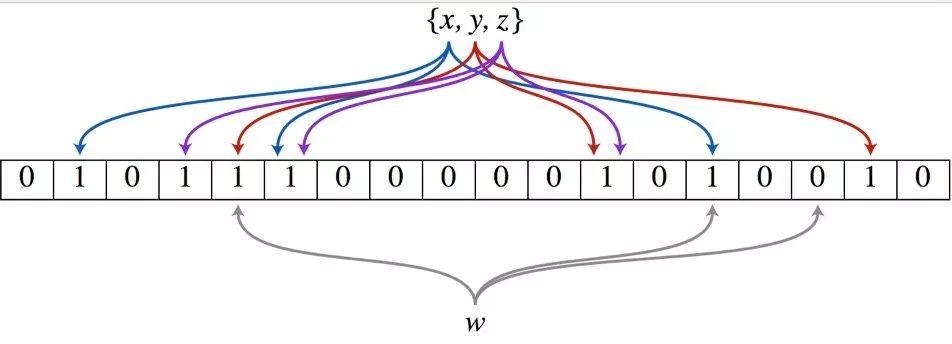
举个例子，假设布隆过滤器有 3 个哈希函数：f1, f2, f3 和一个位数组 arr。现在要把 2333 插入布隆过滤器中：

•对值进行三次哈希计算，得到三个值 n1, n2, n3。•把位数组中三个元素 arr[n1], arr[n2], arr[3] 都置为 1。

当要判断一个值是否在布隆过滤器中，对元素进行三次哈希计算，得到值之后判断位数组中的每个元素是否都为 1，如果值都为 1，那么说明这个值在布隆过滤器中，如果存在一个值不为 1，说明该元素不在布隆过滤器中。

拜托，面试官别问我「布隆」了（修订补充版）

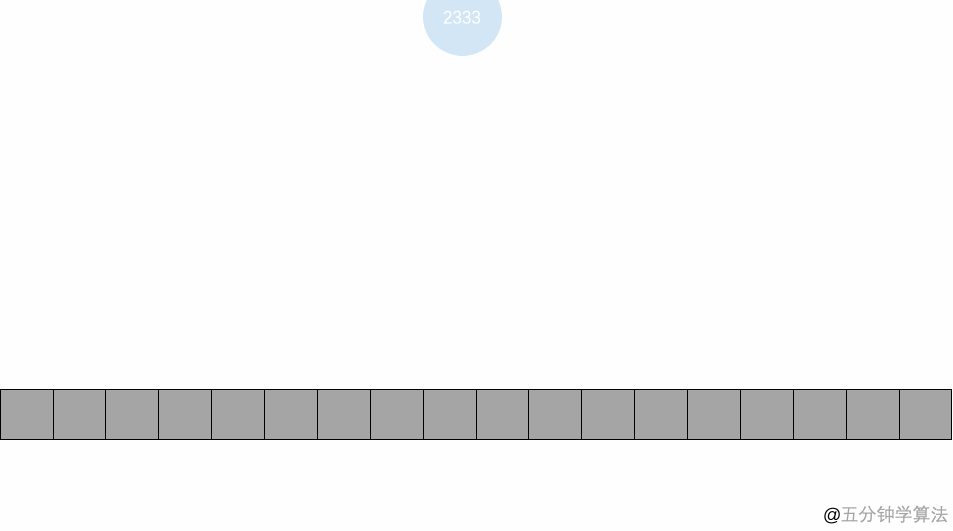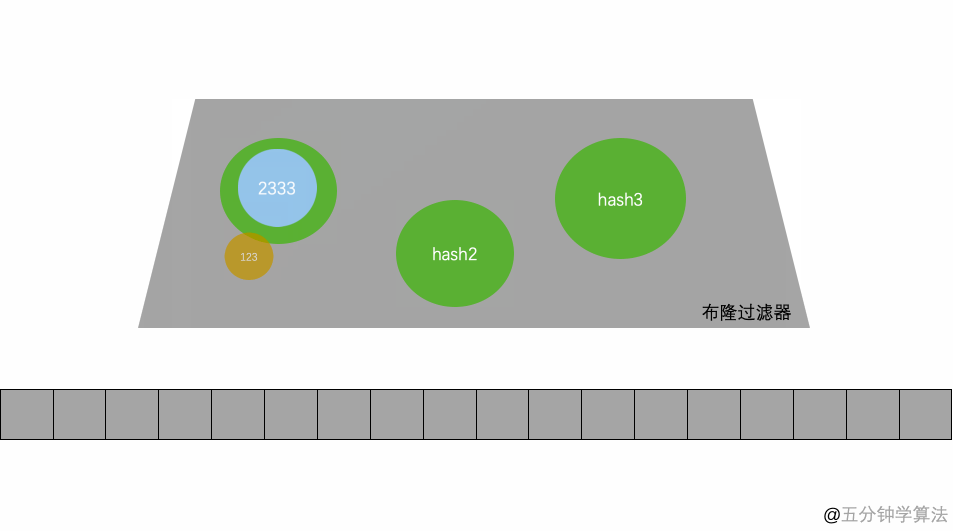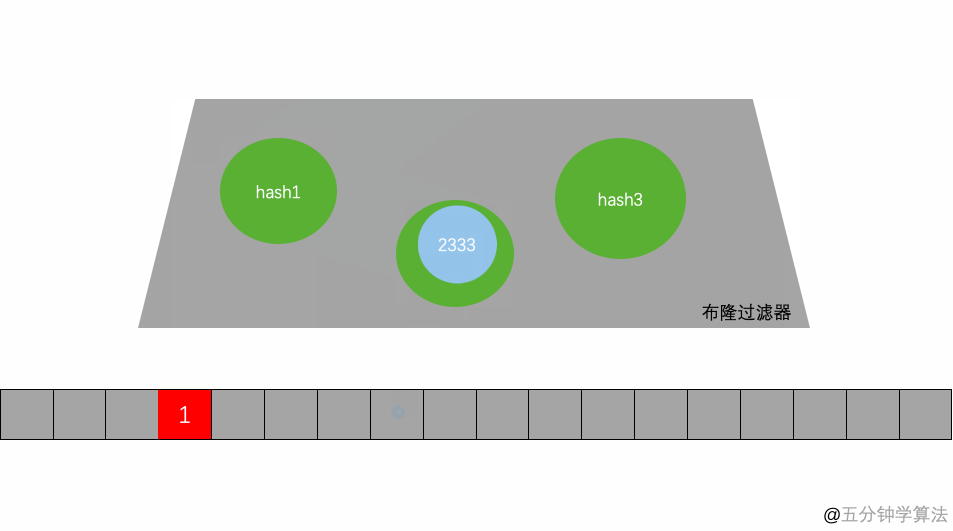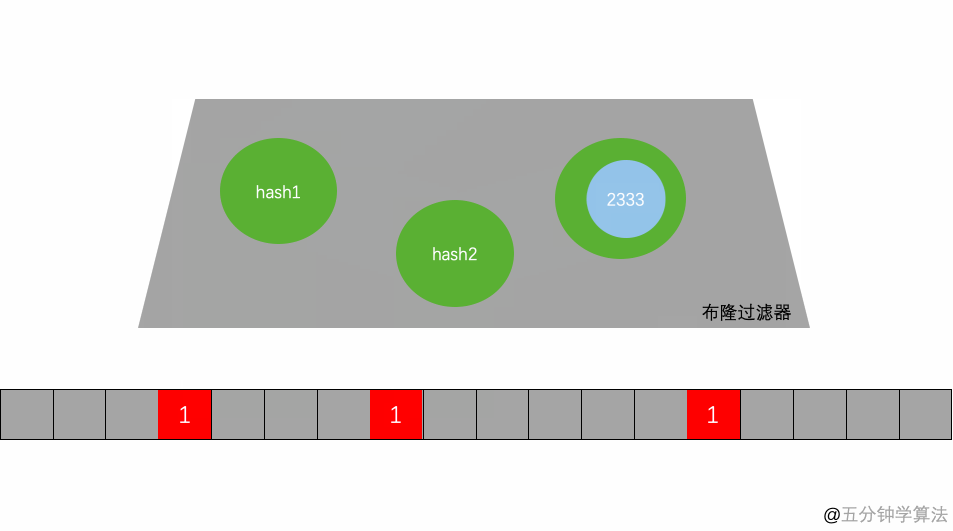
很明显，数组的容量即使再大，也是有限的。那么随着元素的增加，插入的元素就会越多，位数组中被置为 1 的位置因此也越多，这就会造成一种情况：当一个不在布隆过滤器中的元素，经过同样规则的哈希计算之后，得到的值在位数组中查询，有可能这些位置因为之前其它元素的操作先被置为 1 了。

如图 1 所示，假设某个元素通过映射对应下标为4，5，6这3个点。虽然这 3 个点都为 1 ，但是很明显这 3 个点是不同元素经过哈希得到的位置，因此这种情况说明这个元素虽然不在集合中，也可能对应的都是 1，这是误判率存在的原因。

所以，有可能一个不存在布隆过滤器中的会被误判成在布隆过滤器中。

这就是布隆过滤器的一个缺陷：存在误判。

但是，如果布隆过滤器判断某个元素不在布隆过滤器中，那么这个值就一定不在布隆过滤器中。总结就是：

•布隆过滤器说某个元素在，可能会被误判•布隆过滤器说某个元素不在，那么一定不在

用英文说就是：False is always false. True is maybe true。

误判率

布隆过滤器可以插入元素，但不可以删除已有元素。其中的元素越多，false positive rate(误报率)越大，但是false negative (漏报)是不可能的。

由于公众号内对于数学公式的排版不太友好，小吴就不在这贴出来了，具体的计算公式可以在网上查找到。

补救方法

布隆过滤器存在一定的误识别率。常见的补救办法是在建立白名单，存储那些可能被误判的元素。比如你苦等的offer 可能被系统丢在邮件垃圾箱（白名单）了。

使用场景

布隆过滤器的最大的用处就是，能够迅速判断一个元素是否在一个集合中。因此它有如下三个使用场景:

•网页爬虫对 URL 的去重，避免爬取相同的 URL 地址•进行垃圾邮件过滤：反垃圾邮件，从数十亿个垃圾邮件列表中判断某邮箱是否垃圾邮箱（同理，垃圾短信）•有的黑客为了让服务宕机，他们会构建大量不存在于缓存中的 key 向服务器发起请求，在数据量足够大的情况下，频繁的数据库查询可能导致 DB 挂掉。布隆过滤器很好的解决了缓存击穿的问题。